Orbital velocity refers to the speed at which an object must travel to stay in orbit.
After observing an apple falling from a tree, Newton pondered whether the moon also falls and why it hasn’t collided with Earth. He later realized that the moon does fall, but it doesn’t crash because it falls at the same rate as the Earth curves. This causes the moon to orbit around Earth.
 (Photo Credit : Pexels)
(Photo Credit : Pexels)
Newton was puzzled by why the moon moves in a circular path instead of a straight line. Galileo previously stated that an object continues in its direction unless acted upon by an external force, which Newton published as his first law of motion. We now know that Earth’s gravity is the external force that continually alters the moon’s trajectory.
Newtown’s Experiment of Thought
To comprehend how gravity achieves this, Newton devised a thought experiment. He imagined a tall mountain with a cannon on top, shooting a cannonball at different speeds. When the cannonball is shot at a low velocity, it follows a small parabola (Why?) and eventually crashes into Earth due to the pull of gravity.

As the cannon shoots the ball at higher velocities, the ball traces longer parabolas, covering both the linear and curved surfaces. Consequently, the ball travels horizontally along the linear surface and vertically while falling on the curved surface.
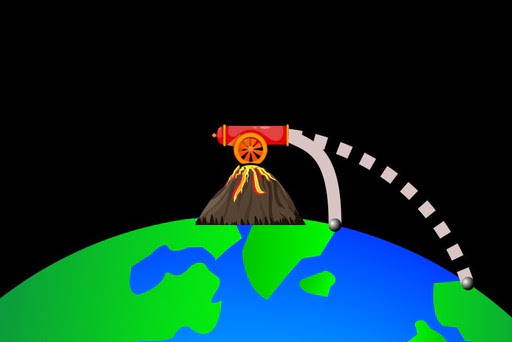
Orbital Velocity
Newton realized that there is a specific velocity at which the ball will never fall. At this velocity, the ball travels only along the linear surface, horizontally, without any vertical movement. This is because as soon as it starts to fall, the Earth beneath it curves, causing the ball to fall at the same rate as the Earth curves. Since these curves form a circle, the ball’s journey eventually ends where it began, successfully completing an orbit. This special velocity is known as orbital velocity.
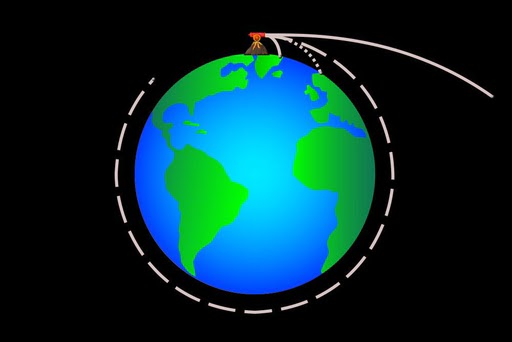
At orbital velocity, the gravitational force of Earth or any celestial body pulls a moon towards its center, similar to the tension exerted on a string that causes a stone attached to the other end to swing in circles around you. This force acts as the centripetal force that drives a moon or satellite in its orbit. It is important to note that the orbit is not a perfect circle but rather an ellipse, similar to Earth’s orbit around the Sun. However, the curvature of both ellipses, or their eccentricity, is so minimal that the orbits appear almost circular.

The expression implies that the velocity of satellites decreases as the distance from the center of Earth increases. This means that satellites closer to Earth’s surface must travel faster than those further away. For example, the moon, which is about 385,000 km away, orbits at a speed of 1.002 km/s, while the International Space Station (ISS), located just 400 km away, completes a lap every 1.5 hours at a speed of 7.67 km/s. Additionally, the velocity of an orbiter is not affected by its mass. This means that whether it is a multimillion-ton moon or a single-gram nail, it must travel at the same velocity to achieve orbit at a given distance from Earth.
It is important to note that satellites, whether natural or artificial, may appear to move horizontally around a planet, but they are actually in a state of perpetual free-fall. As a result, they are weightless, although they still have mass. For instance, the moon weighs hundreds of millions of tons on Earth, but in space, it has no weight and neither does the ISS. This is why the astronauts on the ISS float even though they are only 400 km above Earth’s surface. This phenomenon is similar to what happens in an un-corded elevator falling through a building, where the inhabitants feel weightless. However, the weight is instantly regained when the elevator hits the ground. In the case of the moon and satellites, they continue to fall endlessly without regaining their weight.
