La razón por la cual la identidad de Euler es considerada el «estándar de oro de la belleza matemática» es porque conecta diferentes ramas de las matemáticas de una manera simple y elegante. La expresión incluye el número de Euler ‘e’, que se utiliza extensivamente en cálculo, y ‘i’, la unidad compleja o imaginaria que es la raíz cuadrada de -1.
Leonhard Euler, un físico del siglo XVIII de Suiza, desarrolló muchos conceptos que son esenciales para las matemáticas modernas. Es considerado uno de los más grandes matemáticos de todos los tiempos debido a sus invaluables contribuciones.
A lo largo de su vida, Euler publicó alrededor de 885 artículos y libros sobre matemáticas y otros temas como filosofía. Incluso después de perder la vista, Euler continuó publicando y comentó humorísticamente: «Ahora tendré menos distracciones». Conocido por su diligencia, Euler compensó la pérdida de visión con su excepcional memoria y cálculos mentales.
 (Crédito de la foto: Jakob Emanuel Handmann / Wikimedia Commons)
(Crédito de la foto: Jakob Emanuel Handmann / Wikimedia Commons)
Euler aprendió lecciones matemáticas de Johann Bernoulli, el principal matemático de esa época. Influenciado por el trabajo de Bernoulli, Euler hizo avances significativos en cálculo, geometría y trigonometría. Sin embargo, su obra más famosa gira en torno a los exponenciales y los números complejos. Desarrolló una expresión que fue votada como «el teorema más hermoso de las matemáticas» en una encuesta en el Mathematical Intelligencer.
La Identidad de Euler
La identidad de Euler es una expresión que se encuentra en el núcleo de la teoría de los números complejos. La expresión plantea una pregunta intrigante: ¿qué sucede con un número positivo cuando lo elevamos a una potencia imaginaria?

¿Por qué es tan importante?
La expresión altamente estimada de Euler es considerada el «estándar de oro de la belleza matemática» porque conecta diferentes ramas de las matemáticas de una manera notablemente simple. El hecho de que represente una profunda verdad matemática fundamental a través de una ecuación de una pulgada deleita a los matemáticos de todo el mundo.
Su atractivo estético proviene de la notable conexión entre identidades matemáticas fundamentales y constantes significativas.
- La expresión incluye el número de Euler ‘e’, la base de los logaritmos naturales ampliamente utilizados en cálculo. Es un número trascendental con un valor de 2.71828….
- Incluye ‘i’, la unidad compleja o imaginaria, que es la raíz cuadrada de -1 o la solución de la ecuación ‘x²+1=0‘. Juega un papel crucial en ingeniería eléctrica y ha proporcionado ideas valiosas en mecánica cuántica.
- Incluye ‘π’, otro número trascendental obtenido dividiendo la circunferencia de un círculo por su diámetro. Su valor es 3.14159… Esta constante no necesita más presentación, ya que es la constante matemática más conocida, presente en todas partes desde la geometría euclidiana hasta la Relatividad General.
- Incluye el primer número natural ‘1’, la identidad multiplicativa: cualquier número multiplicado por esta identidad permanece igual.
- Incluye el primer número entero ‘0’, la identidad aditiva: cualquier número sumado a esta identidad permanece igual.
Así, combina cinco constantes fundamentales en las matemáticas.
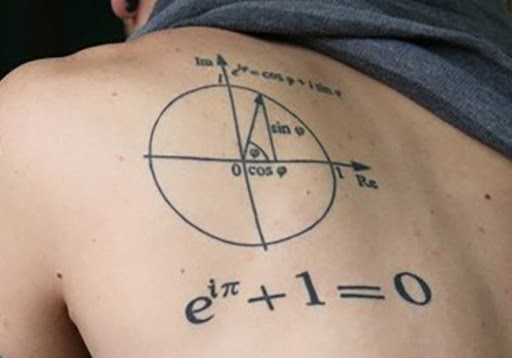
Embelesado por este simple teorema, un profesor de matemáticas en la Universidad de Stanford lo comparó con un soneto de Shakespeare que captura la verdadera esencia del amor o una pintura que revela la belleza de la forma humana que va más allá de la apariencia superficial. Incluso Richard Feynman no pudo resistirse a referirse a él como nuestra joya preciosa y la fórmula más extraordinaria en matemáticas.
En una encuesta realizada por Physics World, la identidad de Euler fue nombrada junto con la ecuación de Maxwell como la mejor ecuación de todos los tiempos. La brillantez de Euler era tan apreciada que en otra encuesta realizada por Mathematical Intelligencer, tres de las cinco expresiones principales fueron atribuidas a Euler.
Prueba:
Podemos derivar la expresión usando dos argumentos. El primer argumento se basa en la teoría de la expansión de las funciones trigonométricas de Taylor, que se basa en los principios del cálculo. La derivación de las secuencias no es relevante en este momento y está más allá del alcance de este artículo.
Originalmente, la operación exponencial de «x elevado a la potencia de y» solo se definía para valores positivos de y, incluidos valores entre 0 y 1, que representaban una raíz de x (como la raíz cuadrada de x). Sin embargo, la expansión de la serie de Taylor conectó dos áreas distintas, dando lugar a lo que ahora se conoce como la fórmula de Euler. Aquellos interesados pueden encontrar una prueba detallada de cómo se derivó la fórmula de Euler aquí.
La identidad de Euler es un caso especial de la fórmula de Euler donde el ángulo es 180º o π radianes, lo que hace que los valores del lado derecho se conviertan en (-1) + 0, lo que se simplifica a -1.
El segundo argumento deriva la fórmula de Euler gráficamente en un plano complejo 2-D. El plano complejo consta de dos ejes: el eje real que representa números reales y el eje complejo que representa números complejos. Un número complejo en este plano se representa como «x + iy».
En este plano, se dibuja un círculo con un radio de 1 unidad con su centro en el origen. Cuando un número complejo, representado por un vector que toca la circunferencia del círculo, se gira hacia el borde del segundo cuadrante, el ángulo que forma con el eje real es de 180º o π radianes.
En el punto donde el vector toca el eje horizontal, sus coordenadas son (-1, 0). Refiriéndose a la forma polar de los números complejos, es fácil ver que
